I am authoring a jQuery plugin to enhance drop down selects;
UFD: The Unobtrusive Fast-filter Drop-down. Try it out easily on your own app with
the bookmarklet. Be amazed. Show your friends.
One of the important requirements was filtering of the the drop down options from the input. The naive way to do this is a linear search through each list item, but this is
way too slow for large lists; the list needs to be re-filtered after every keystroke.
I decided on a
Trie implementation, which gives great prefix search performance. A Trie stores objects on a tree, constructed by slicing the key-string for each object into characters. Starting at the root, each character maps to a node - see the incoming vertex in the diagram below.
Each node has a map of character to child nodes, and an optional target object. Target objects are placed where the chain of characters maps to the objects key, so you can easily traverse the nodes with a key-string to find a given the target object. The structure is a tree, but the path to a given object is similar to a linked list of each character in the key string.
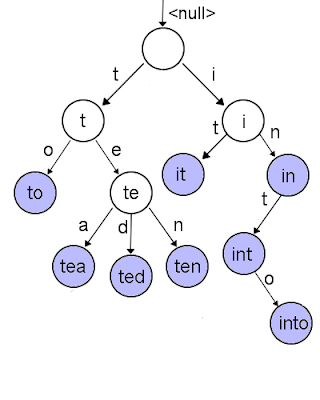
The blue nodes are ones that have objects on them - in this example we see the words:
to,tea,ted,ten,it,int,into. Notice how objects are on the leaf nodes, unless their key is a substring of another key.
It is easy to see how we can do quick prefix searching:start at the root node (which represents the empty string) and traverse the nodes, consuming each character of the key prefix string. Once the prefix key string is consumed, that subtree has all the matches of the given key prefix.
But what if we want to find all nodes that have a given key
infix? After failing to find a better data structure, I decided to hack an extension to the data structure.
Is there a better data structure that I should be using? Suggestions welcome. Anyway:
Instead of starting at the root node, we need an array of start points. During creation I put a reference to each new node in a list. There is one list for every unique character across the whole key set. This means that
each list has references to all nodes of that character. These lists of start points are called the infixRoots.
Yes, some of these lists could be quite large. For example, the "e" list for a 1000-item list may have over 1000 items.
Lets look at a filtering example: lets search for the objects that match the infix key "to".

We start by getting the infix list matching the start character ("t") from the infixRoots set. The highlighted nodes and all of their child nodes, by definition, have "t" in their key - no surprises there.
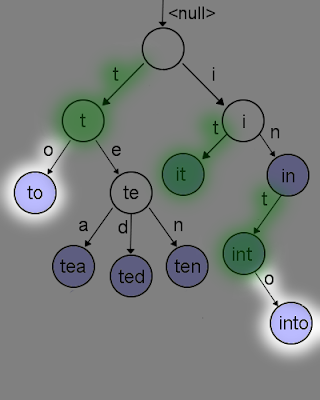
We next iterate over the that list of "t" nodes, creating a new list with child nodes that match the next character; "o". Any node without a match is not added to the new list. We keep iteratively mapping node lists from one character to the next, until we consume the infix keys' characters.
The nodes left in the final set,
and all of their child nodes, all are matches. Iterate over each subtree and get the attached objects. In our example above, the nodes representing
to,into are found. Had the key
top been in the tree, it would also match, as it would be a child of
to.
Have a look at the
javascript implementation for UFD, the InfixTrie is a self-contained prototype inside the source near the bottom.






